Backpropagation From Scratch

This post is an archive of an article I wrote on March 11th, 2014.

This article is based off of a file in my github repository which should help clarify some things that were hard to explain using comments alone. We will be making a Neural Network that implements the backpropagation algorithm. This will not be a framework, but rather a really simplistic look at what goes on under the hood. The topology will be hard-coded and the whole program should be roughly 40 lines of code. I am using C#, however, it would be almost identical in any number of other languages since it's basically just math and a few arrays :)

The Class

Just to make the sample complete, I'll show you the basic class outline. From here, we'll be adding functions to it, so just assume all code henceforth will be included in this class. We only need 3 variables and 1 constant, so that will be the first few lines.

Note: I seed the random with something for consistency when testing. This let's me know whether it's producing the correct output, since it will always react the same way each time we run the program.

public class FastNet
{
    const float LEARN_RATE = 0.5f;

    Random rand = new Random(424242);
    float[] weights;
    float[] outputs;
}

The Constructor

Let's talk about weights. At its' core, a Neural Network is a summation machine. You feed it a number of inputs, allow it to perform some transformations, and then watch as it pushes the output of each node down the rabbit hole.

One of the transformations a Neural Network typically will do is to multiply whatever input values it receives against a weight (in this example, we define a weight as a floating-point number between -1 and 1, exclusive). Once we've summed up all the inputs times all the weights (within a given node), we run this value through an activation function and then push it further down. I'll go into more detail later, but today we will be using the sigmoid function which is capable of taking any real number and consolidating it into a value between 0 and 1 (if you're a math major, I'm sure this is not 100% technically accurate... so I apologize!)

I've read many descriptions about how to visualize neural networks. My favorite has always been thinking of it like a brain. Each node in the graph is a neuron that may or may not 'fire'. In our network, all nodes will fire - it's just a matter of how 'strongly' (how large the output is).

This is how our weights will work, but before we get there - we've got to set them up first! Following is the simple code to setup our variables.

public FastNet()
{
    weights = new float[10];
    outputs = new float[5];
    for (int i = 0; i < weights.Length; i++)
        weights[i] = (float)(rand.NextDouble() - rand.NextDouble());
}

Function 1 - getOutput

This first function will compute the output of our Neural Network. Keep in mind that Neural Networks are graphs, where each node is structured such that each node above connects to every node immediately below. Also known as a many-to-many graph. If you draw out the graph on paper, you would see how each of the weights and inputs and outputs are feeding into each other (I have a picture further down which better demonstrates this). Here's the code for calculating the output:

public float getOutput(float[] input)
{
    outputs[0] = sig(input[0] * weights[0] + input[1] * weights[1]);
    outputs[1] = sig(input[0] * weights[2] + input[1] * weights[3]);
    outputs[2] = sig(outputs[0] * weights[4] + outputs[1] * weights[5]);
    outputs[3] = sig(outputs[0] * weights[6] + outputs[1] * weights[7]);
    outputs[4] = sig(outputs[2] * weights[8] + outputs[3] * weights[9]);

    return outputs[4];
}

There are a few important things to note which had me confused me for quite some time. Firstly, if your graph has two inputs - that means each node within your input layer gets two connections. So 2 input layer nodes does not mean 1 input per node. It means however many inputs you want to support will be feed into each of the nodes in your input layer.

Another thing to realize is, this graph sports a many-to-many connection arrangement but it doesn't have to be like that. I've never tried anything else, but from what I've read - it's possible to go crazy with your network topology. This is just one method and, arguably, the most straightforward.

Another thing to notice is that, when feeding values further down the graph, we are running them through our activation function first. This is crucial because, later one, we take the derivative of our activation function and use that to calculate the error with respect to a given weight. This is "elementary" calculus, but don't be scared if you're not familiar with crazy math. Just understanding the basic concepts are enough.

With the function above, you will be able to successfully evaluate a given input. Note: it might be a good idea to make sure the input is exactly 2 elements long, otherwise you won't get what you expect back.

Function 2 - train

The next item on our list is a function to train the Neural Network.

public void train(float[] input, float target)
{
    float[] errors = new float[outputs.Length];
    float output = getOutput(input);

    errors[4] = output * (1f - output) * (target - output);
    errors[3] = outputs[3] * (1f-outputs[3]) * (errors[4] * weights[9]);
    errors[2] = outputs[2] * (1f-outputs[2]) * (errors[4] * weights[8]);
    errors[1] = outputs[1]*(1f-outputs[1])*((errors[3]*weights[7]) + (errors[2]*weights[5]));
    errors[0] = outputs[0]*(1f-outputs[0])*((errors[3]*weights[6]) + (errors[2]*weights[4]));

    weights[9] += LEARN_RATE * outputs[3] * errors[4];
    weights[8] += LEARN_RATE * outputs[2] * errors[4];
    weights[7] += LEARN_RATE * outputs[1] * errors[3];
    weights[6] += LEARN_RATE * outputs[0] * errors[3];
    weights[5] += LEARN_RATE * outputs[1] * errors[2];
    weights[4] += LEARN_RATE * outputs[0] * errors[2];
    weights[3] += LEARN_RATE * input[1] * errors[1];
    weights[2] += LEARN_RATE * input[0] * errors[1];
    weights[1] += LEARN_RATE * input[1] * errors[0];
    weights[0] += LEARN_RATE * input[0] * errors[0];
}

We're doing a lot of things at once here, so let's take it in pieces.

Calculating the Error

If you think of the graph as one large function (which it is), you would represent it in a fashion similar to: layer1( layer2( layer3() ) ) - right? Each layer is computed, and various values from that layer get pushed down the pipeline. With backpropagation, we ultimately want to update our weights so they can start to converge on a given value. If you consider the fact that some weights may have computed a 'better' value than others - it becomes clear that you cannot update the whole graph based on the difference between output and target value. Instead, you need to evaluate each node to see how badly its' output affected the graph as a whole.

To do this, we start at the bottom of the network. To use my prior example, we figure out the blame for layer3() and push it back up to layer2() and push that back up to layer1(). The closer to our input layer that we get, the less blame a given node will receive.

So that's what we're doing in the first few lines of our train function. You may notice the output node has a different calculation than the rest. This is because every node in the output layer (no matter how big it is) will always receive the same blame, which is essentially how far off the entire network is as a whole.

Training the Network

The latter 10 (or so) lines of code use the error that we calculated to update each weight appropriately. The adjustment is equal to the LEARN_RATE constant times the output of the node that encapsulates the weight times the error of the node that utilized the weight. Here's a picture of my white board to try and help explain this a little better.

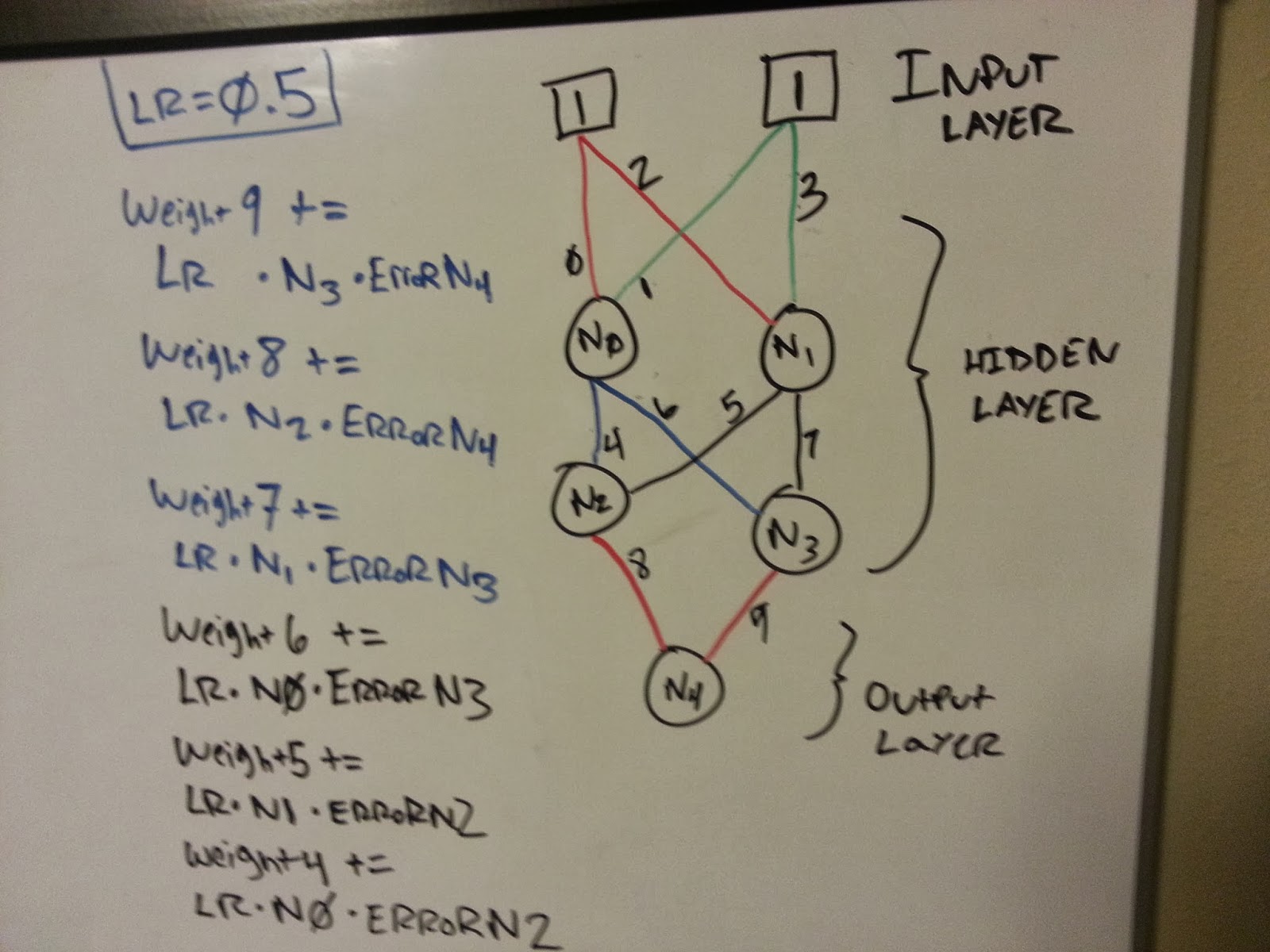
As you can see, each connection in my network has a number which represents the weight array index. Hopefully this will help you visualize what the network looks like and how each of the weights are used. With this in mind, take a look at the left side of the white board. That is a hand-written example of the adjustment part in the train() method.

This network is modeled after our program. There may be an easier way to assign the weights, but this was what naturally occurred when I went to design the neural network. I will say that attempting to expound upon this code to create a network that is not of a hard-coded topology is proving to be very challenging. I'm working on that next, however, and hope to publish another article that shows how to create a scalable version of this code.

Sigmoid

To complete the neural network, we need to implement one last function - the sigmoid helper function.

private float sig(float val)
{
    return (float)(1.0f / (1.0f + Math.Exp(-val)));
}

Conclusion

And that's it! If you put all of this code together, you will have a working Neural Network that is capable of running through the XOR challenge. From here, the sky is the limit! I hope you found this tutorial useful. Machine Learning is a passion of mine, and I hope to contribute more knowledge in future posts - so stay tuned!